


CIRCUITO
RL SERIE
En un circuito RL serie en corriente
alterna, se tiene una resistencia y una bobina en serie. La corriente en amboselementos es la misma.
La tensión en la bobina está en fase con la corriente (corriente alterna) que pasa por ella (tienen sus
valores máximos simultáneamente).
Pero el voltaje en
la bobina está adelantado a la corriente que pasa por ella en 90º (la tensión
tiene su valor máximo antes que la corriente)
El valor de la fuente
de voltaje que alimenta este circuito esta dado por las siguientes fórmulas:
- Voltaje (magnitud) VS = (VR2 + VL2)1/2
- Angulo = /Θ = Arctang (Vl/VR).
- Voltaje (magnitud) VS = (VR2 + VL2)1/2
- Angulo = /Θ = Arctang (Vl/VR).
Estos valores se expresan en forma demagnitud y
ángulo. Ver el diagramafasorial de tensiones
Ejemplo: 47 /30° que
significa que tiene magnitud de 47 y ángulo de 30 grados
La impedancia Z sería la suma (suma fasiorial) de la resistencia y la reactancia inductiva. Y se puede
calcular con ayuda de la siguiente fórmula:
Para obtener la magnitud de Z de dividen los valores de Vs e I
Para obtener el /Θ de Z se resta el ángulo de la corriente, del ángulo del voltaje.
Para obtener el /Θ de Z se resta el ángulo de la corriente, del ángulo del voltaje.
Nota: lo que está incluido en paréntesis elevado a la 1/2,
equivale a la raíz cuadrada.
CIRCUITO RL PARALELO
En un circuito RL paralelo, el valor de voltaje es el mismo para la resistencia y para la bobina. Ver el siguiente diagrama
V = VR = VL
La corriente que pasa por la resistenciaestá en fase con el voltaje aplicado.
(El valor máximo de voltaje coincide con el valor máximo de
corriente).
En cambio en la bobina la corriente se atrasa 90º con respecto al voltaje. (el valor máximo devoltaje sucede antes que el valor máximo de la
corriente)
La corriente total que alimenta este circuito se puede obtener con ayuda de las
siguientes fórmulas:
- Corriente (magnitud)
It = (IR2 + IL2)1/2
- Angulo Θ = Arctang (-IL/IR)
- Angulo Θ = Arctang (-IL/IR)
Ver el diagrama fasorial y de corrientes
La impedancia (Z) se obtiene con ayuda de la siguiente
fórmula:
¿Cómo se logra lo anterior?
- Para obtener la magnitud de Z dividen las magnitudes de Vs e It para obtener la magnitud de la impedancia
- Para obtener el /Θ de Z se resta el ángulo de la corriente del
de voltaje para obtener el ángulo de la
impedancia.
Nota: lo que está incluido en paréntesis elevado a la 1/2,
equivale a la raíz cuadrada.
CIRCUITO
RC EN SERIE
En un circuito RC en serie la corriente (corriente alterna) que pasa por la resistor y por el capacitor es la misma
El voltaje entregado VS es igual a la suma fasorial de la
caída de voltaje en el resistor (Vr) y de la caìda de voltaje en el capacitor (Vc). Ver la
siguiente fórmula: Vs = Vr + Vc (suma fasorial)
Esto significa que cuando la corriente está en su punto más alto
(corrientepico), será así tanto en el resistor como en el capacitor.
Pero algo diferente pasa con los voltajes. En el
resistor, el voltaje y lacorriente están en fase (sus valores máximos y mínimos coinciden en el tiempo). Pero el voltaje en el capacitor no es así.
Como el capacitor se opone a cambios bruscos de voltaje, el voltaje en
el capacitor está retrasado con respecto a la corriente que pasa por
él. (el valor máximo
de voltaje en el capacitor sucede después
del valor máximo de corriente en 90o).
Estos 90º equivalen a ¼ de la longitud de onda dada
por la frecuencia de lacorriente que está pasando por el circuito.
El voltaje total que alimenta el circuito RC
en serie es igual a la suma
fasorial del voltaje en el resistor y el voltaje en el capacitor.
Valor del voltaje (magnitud): Vs = ( VR2 + VC2 )1/2
Angulo de desfase Θ = Arctang (-VC/VR)
Angulo de desfase Θ = Arctang (-VC/VR)
Como se dijo antes
- La corriente adelanta al voltaje en un capacitor en 90°
- La corriente y el voltaje están en fase en un resistor.
- La corriente adelanta al voltaje en un capacitor en 90°
- La corriente y el voltaje están en fase en un resistor.
Con ayuda de estos datos se construye el diagrama fasorial y el triángulo de
voltajes.
De estos gráficos de obtiene la magnitud y ángulo de la fuente de alimentación (ver fórmulas anteriores):
A la resistencia total del conjunto
resistor-capacitor, se le llama impedancia (Z) (un nombre más
generalizado) y Z es la suma fasorial (no una suma directa) de los valores del resistor y de la
reactancia del capacitor. La unidad de la impedancia es el "ohmio".
La impedancia (Z) se obtiene con ayuda de la
siguiente fórmula:
- Vs: es la magnitud del voltaje
- Θ1: es el ángulo del voltaje
- I:es la magnitud de la corriente
- Θ2: es el ángulo de la corriente
¿Cómo se aplica la fórmula?
La impedancia Z se obtiene dividiendo directamente
Vs e I y el ángulo (Θ) de Z se obtiene restando el ángulo de I del ángulo Vs.
El mismo triángulo de voltajes se puede utilizar si a cada
valor (voltajes) del triángulo lo dividimos por el valor de lacorriente (corriente es igual en todos los elementos en una conexión serie), y así se obtiene el triángulo
de impedancia
Nota: lo que está incluido en paréntesis elevado a
la 1/2, equivale a la raíz cuadrada.
CIRCUITO RC EN PARALELO
En un circuito RC en paralelo el valor de la tensión es el mismo en el condensador y en la resistencia y la corriente (corriente alterna) que
la fuente entrega al circuito se divide entre la resistencia y el condensador. (It = Ir + Ic)
Ver el primer diagrama abajo.
La corriente que pasa por la resistenciay la tensión que hay en
ella están en fase debido a que la resistencia no causa desfase.
La corriente en el capacitor está adelantada con respecto a la
tensión (voltaje), que es igual que decir que
elvoltaje está retrasado con
respecto a la corriente.
Como ya se sabe el capacitor se opone a cambios bruscos
de tensión.
La magnitud de la corriente alterna total
es igual a la suma de las corrientes por los dos elementos y se obtiene con
ayuda de las siguientes fórmulas:
- Magnitud de la corriente (AC) total:
It = (Ir2 + Ic2)1/2
It = (Ir2 + Ic2)1/2
- Angulo de desfase:
Θ = Arctang (-Ic/Ir)
Θ = Arctang (-Ic/Ir)
Ver el siguiente diagrama fasorial de corrientes:
La impedancia Z del circuito en paralelo se obtiene con la fórmula:
¿Cómo se aplica la fórmula?
Z se obtiene dividiendo directamente V e I y el ángulo (Θ) de Z se
obtiene restando el ángulo de I del ángulo V. Este ángulo es el mismo que
aparece en el gráfico anterior y se obtiene con la formula: Θ = Arctang
(-Ic/Ir)
Nota: lo que está incluido en paréntesis elevado a la 1/2,
equivale a la raíz cuadrada.
CIRCUITO RLC SERIE
Cuando se conecta un circuito RLC enserie, alimentado por una señal alterna(fuente de
tensión de corriente alterna),
hay un efecto de ésta en cada uno de los componentes.
En el condensador aparecerá una reactancia capacitiva, y
en la bobina una reactancia inductiva, dadas por las siguientes fórmulas:
XL = 2 x π x f x L
XC = 1 / (2 x π x f x C)
XC = 1 / (2 x π x f x C)
Donde:
π = 3.14159
f = frecuencia en Hertz
L = Valor de la bobina en henrios
C = Valor del condensador en faradios
π = 3.14159
f = frecuencia en Hertz
L = Valor de la bobina en henrios
C = Valor del condensador en faradios
Como se puede ver los valores de estas
reactancias depende de la frecuencia de la fuente.
A mayor frecuencia, XL es mayor, pero XC es menor y viceversa.
Hay una frecuencia para la cual el valor de la XC y XL son
iguales. Esta frecuencia se llama frecuencia
de resonancia y se obtiene de
la siguiente fórmula:
FR = 1 / (2 x π x (L x C)1/2)
En resonancia como los valores de XC y XL son
iguales, se cancelan y en un circuito
RLC enserie la impedancia que ve la fuente es el valor de la resistencia. A frecuencias menores a
la de resonancia, el valor de la reactancia capacitiva es grande y la
impedancia es capacitiva
A frecuencias superiores a la de resonancia, el valor de la reactancia
inductiva crece y
la impedancia es inductiva.
Nota: es importante visualizar que los efectos de la reactancia
capacitiva y la inductiva son opuestos, es por eso que se cancelan y causan la
oscilación (resonancia)
El Ancho de banda (BW) y el Factor de calidad (Q)
Los circuitos resonantes son utilizados para seleccionar bandas de
frecuencias y para rechazar otras. Cuando se está en la frecuencia de
resonancia la corriente por el circuito es máxima.
En la figura: A una corriente menor (70.7% de la máxima), la
frecuencia F1 se llama frecuencia baja de corte o frecuencia baja de potencia
media. La frecuencia alta de corte o alta de potencia media es F2.
El ancho de banda de este circuito está entre estas dos frecuencias y se
obtiene con la siguiente fórmula: Ancho Banda = BW = F2 - F1
El factor de calidad (Q) o factor Q es:
Q = XL/R o XC/R
Q = XL/R o XC/R
También la relacionándolo con el Ancho Banda:
Q = frecuencia resonancia / Ancho banda = FR/BW
Q = frecuencia resonancia / Ancho banda = FR/BW
Ejemplos:
- Si F1 = 50 Khz y F2 = 80 Khz, FR = 65 Khz, el factor de calidad es: Q = FR / BW = 65 / (80-50) = 2.17
- Si F1 = 60 Khz y F2 = 70 Khz, FR = 65 Khz, el factor de calidad es: Q = FR / BW = 65 / (70-60) = 6.5
- Si F1 = 50 Khz y F2 = 80 Khz, FR = 65 Khz, el factor de calidad es: Q = FR / BW = 65 / (80-50) = 2.17
- Si F1 = 60 Khz y F2 = 70 Khz, FR = 65 Khz, el factor de calidad es: Q = FR / BW = 65 / (70-60) = 6.5
Se puede observar que el factor de calidad es mejor a menor ancho
de banda. (el circuito es más selectivo)
CIRCUITO RLC PARALELO
Cuando se conecta un circuito RLC(resistencia, bobina y condensador en paralelo, alimentado por una señalalterna (fuente de
tensión de corriente alterna, hay
un efecto de ésta en cada uno de los componentes.
En el condensador o capacitor aparecerá una reactancia
capacitiva, y en la bobina o inductor una reactancia inductiva, dadas por las
siguientes fórmulas:
XL = 2 x π x f x L
XC = 1 / (2 x π x f x C)
XC = 1 / (2 x π x f x C)
Donde:
π = Pi = 3.14159
f = frecuencia en Hertz
L = Valor de la bobina en henrios
C = Valor del condensador en faradios
π = Pi = 3.14159
f = frecuencia en Hertz
L = Valor de la bobina en henrios
C = Valor del condensador en faradios
Como se puede ver los valores de estas
reactancias depende de la frecuencia de la fuente.
A mayor frecuencia XL es mayor, pero XC es menor y viceversa. Hay
una frecuencia para la cual el valor de la XC y XL son iguales.
Esta frecuencia se llama: frecuencia
de resonancia y se obtiene de
la siguiente fórmula: FR = 1 / (2 x π x (L x C)1/2)
En resonancia como los valores de XC y XL son iguales, se cancelan y en uncircuito RLC en paralelo la impedancia que ve la fuente es el valor de la resistencia.
- A frecuencias menores a la de resonancia, el valor de la
reactancia capacitiva es alta y la inductiva es baja.
- A frecuencias superiores a la de resonancia, el valor de la
reactancia inductiva es alta y la capacitiva baja.
Como todos los elementos de una conexión en paralelo tienen el
mismovoltaje, se puede encontrar la corrienteen cada elemento con ayuda de
la Ley de Ohm. Así:
IR = V/R, IL = V/XL, IC = V/XC
La corriente en la resistencia está en fase con la tensión, la corriente en la bobina está atrasada 90° con
respecto al voltaje y la corriente en el condensador está adelantada en 90°.
Nota: Es importante visualizar que los efectos de la reactancia
capacitiva y la inductiva son opuestos, es por eso que se cancelan y causan la
oscilación (resonancia)
El ancho de banda (BW) y el Factor de calidad (Q)
Los circuitos resonantes son utilizados para
seleccionar bandas de frecuencias y para rechazar otras. Cuando se está en la
frecuencia de resonancia la corriente por el circuito es máxima.
En la figura: A una corriente menor (70.7% de la máxima), la
frecuencia F1 se llama frecuencia baja de corte o frecuencia baja de potencia media.
La frecuencia alta de corte o alta depotencia media
es F2. El ancho de banda de este circuito está entre estas dos frecuencias y se
obtiene con la siguiente fórmula:
Ancho Banda = BW =
F2 - F1
También relacionándolo con el Ancho Banda:
Q = frecuencia de resonancia / Ancho de banda = FR / BW
Ejemplos:
Si F1 = 50 Khz, F2 = 80 Khz, FR = 65 Khz.
El factor de calidad es: Q = FR / BW = 65 / (80-50) = 2.17
Si F1 = 50 Khz, F2 = 80 Khz, FR = 65 Khz.
El factor de calidad es: Q = FR / BW = 65 / (80-50) = 2.17
Si F1 = 60 Khz y F2 = 70 Khz, FR = 65 Khz.
El factor de calidad es: Q = FR / BW = 65 / (70-60) = 6.5
El factor de calidad es: Q = FR / BW = 65 / (70-60) = 6.5
Se puede observar que el factor de calidad es mejor a menor ancho de banda. (el circuito es mas selectivo)
Frecuencia
es una magnitud que mide el número de repeticiones por unidad de tiempo de cualquier fenómeno o suceso periódico.
Para calcular la frecuencia de un suceso, se contabilizan un número de ocurrencias de este teniendo en cuenta un intervalo temporal, luego estas repeticiones se dividen por el tiempo transcurrido. Según el Sistema Internacional (SI), la frecuencia se mide en hercios (Hz), en honor a Heinrich Rudolf Hertz. Un hercio es la frecuencia de un suceso o fenómeno repetido una vez por segundo. Así, un fenómeno con una frecuencia de dos hercios se repite dos veces por segundo. Esta unidad se llamó originariamente «ciclo por segundo» (cps). Otras unidades para indicar la frecuencia son revoluciones por minuto (rpm). Las pulsaciones del corazón y el tempo musical se miden en «pulsos por minuto» (bpm, del inglés beats per minute).
Un método alternativo para calcular la frecuencia es medir el tiempo entre dos repeticiones (periodo) y luego calcular la frecuencia (f) recíproca de esta manera:
donde T es el periodo de la señal.
Período
Este término se utiliza regularmente para designar al intervalo de tiempo necesario para completar un ciclo repetitivo, o simplemente el espacio de tiempo que dura algo.
- En geología, período geológico es una unidad del tiempo geológico de segundo orden, inferior a la era geológica y superior a la época geológica.3
- También existen periodos geológicos en cuerpos celestes externos a la Tierra (véase Escala de tiempo geológico lunar).
- En matemáticas:
- El período y la frase organizados en una o más oraciones (periódico puro) o posteriormente al primer número decimal (periódico mixto).
- El período de una función periódica es la parte de ésta (P) que, conforme se le añade a la variable independiente, hace repetir los valores de la variable dependiente:
- En física, período de oscilación es el intervalo de tiempo entre 2 puntos equivalentes de una onda u oscilación, también se puede asociar a la frecuencia mediante la relación:
Amplitud
Es una perturbación física que se propaga en el espacio como una onda armónica puede modelizarse matemáticamente como una magnitud física 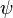 cuyo valor varía con el tiempo y de un punto a otro del espacio según una ecuación como:
cuyo valor varía con el tiempo y de un punto a otro del espacio según una ecuación como:
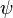 cuyo valor varía con el tiempo y de un punto a otro del espacio según una ecuación como:
cuyo valor varía con el tiempo y de un punto a otro del espacio según una ecuación como:
Donde  es la velocidad de propagación de la perturbación. Para una onda plana que se propaga en dirección x la solución de la ecuación anterior es:
es la velocidad de propagación de la perturbación. Para una onda plana que se propaga en dirección x la solución de la ecuación anterior es:
 es la velocidad de propagación de la perturbación. Para una onda plana que se propaga en dirección x la solución de la ecuación anterior es:
es la velocidad de propagación de la perturbación. Para una onda plana que se propaga en dirección x la solución de la ecuación anterior es:
Y en ese caso la amplitud se define como:
Usualmente la intensidad de una onda es una magnitud proporcional al promedio del cuadrado de la amplitud:
Para una onda periódica de período T:
Longitud de onda.
La distancia existente entre dos crestas o valles consecutivos es lo que llamamos longitud de onda. La longitud de onda de una onda describe cuán larga es la onda. Las ondas de agua en el océano, las ondas de aire, y las ondas de radiación electromagnética tienen longitudes de ondas. La longitud de onda representa la distancia real recorrida por una onda que no siempre coincide con la distancia del medio o de las partículas en que se propaga la onda.
Ciclo
en corriente alterna el valor va de positibo a negativo
en una onda
un ciclo es.cuando pasa a ser una vez negatovo y otra positibo
un siclo es igual a un Hz
en mexico unamos 60Hz por segundo que es la velocidad de cambio
de polaridad de la corriente fase
,La electricidad, tanto industrial como domestica, la distribuyen, por cuestiones que mejor es no meterse ahora en tanto embrollo, en tres fases y un neutro, o sea; es trifásica, es así porque la producción de este elemento se hace con unas bobinas que están desfasadas, como mínimo 120º, no es exactamente así puesto que la hacen pares o tríos de bobinas en serie en paquetes de desfase 30º, así la corriente es mas plana y se conduce mejor sin perdidas, entonces una fase es coger una fase de estas que se suelen llamar R,S,T y el neutro con ello se consigue 120 V; hoy en día al ser la mayoría de electrodomésticos confeccionados en estrella el neutro se queda en la puerta de la toma general, se toman dos fases cualquiera y ya tenemos 220 v de tensión, en la distribución de la energía en una planta de viviendas se hace de una manera equitativa, a fin de no cargar una linea demasiado y otras trabajar poco con lo que se descompensaría provocando averías, así si un edificio tiene 30 plantas 10 son con R y T 10 con R y S y las otras diez con T y S, es una manera de compensar la linea
Desfaso O Diferencia De Faso
Desfase (o desfasaje en algunos países) entre dos ondas es la diferencia entre sus dos fases. Habitualmente, esta diferencia de fases, se mide en un mismo instante para las dos ondas, pero no siempre en un mismo lugar del espacio.
El desfase también es una fase del proceso de petaje,un proceso cíclico que practicamente esta en todas las tareas diarias y que define el inicio y el fin de las mismas.
Valores Instantaneos
-Es el valor que toma la tensión en cada instante de tiempo.
Si v=V0 sen(wt), a cada valor de t le corresponde uno de v instantáneo.
FUENTE: http://electrictangarife.blogspot.com/p/electrotecnia-xd.html
valores significativos
A continuación se indican otros valores significativos de una señal sinusoidal:
- Valor instantáneo (a(t)): Es el que toma la ordenada en un instante, t, determinado.
- Valor pico a pico (App): Diferencia entre su pico o máximo positivo y su pico negativo. Dado que el valor máximo de sen(x) es +1 y el valor mínimo es -1, una señal sinusoidal que oscila entre +A0 y -A0. El valor de pico a pico, escrito como AP-P, es por lo tanto (+A0)-(-A0) = 2×A0.
- Valor medio (Amed): Valor del área que forma con el eje de abscisas partido por su período. El valor medio se puede interpretar como el componente de continua de la oscilación sinusoidal. El área se considera positiva si está por encima del eje de abscisas y negativa si está por debajo. Como en una señal sinusoidal el semiciclo positivo es idéntico al negativo, su valor medio es nulo. Por eso el valor medio de una Oscilación sinusoidal se refiere a un semiciclo. Mediante el cálculo integral se puede demostrar que su expresión es la siguiente;
- Pico o cresta: Valor máximo, de signo positivo (+), que toma la oscilación sinusoidal del espectro electromagnético, cada medio ciclo, a partir del punto “0”. Ese valor aumenta o disminuye a medida que la amplitud “A” de la propia oscilación crece o decrece positivamente por encima del valor "0".
- Valor eficaz (A): El valor eficaz se define como el valor de una corriente (o tensión) continua que produce los mismos efectos calóricos que su equivalente de alterna. Es decir que para determinada corriente alterna, su valor eficaz (Ief) será la corriente continua que produzca la misma disipación de potencia (P) en un resistor (R). Matemáticamente, el valor eficaz de una magnitud variable con el tiempo, se define como la raíz cuadrada de la media de los cuadrados de los valores instantáneos alcanzados durante un período:
En la literatura inglesa este valor se conoce como R.M.S. (root mean square, valor cuadrático medio), y de hecho en matemáticas a veces es llamado valor cuadrático medio de una función. En el campo industrial, el valor eficaz es de gran importancia, ya que casi todas las operaciones con magnitudes energéticas se hacen con dicho valor. De ahí que por rapidez y claridad se represente con la letra mayúscula de la magnitud que se trate (I, V, P, etc.). Matemáticamente se demuestra que para una corriente alterna sinusoidal el valor eficaz viene dado por la expresión:
El valor A, tensión o intensidad, es útil para calcular la potencia consumida por una carga. Así, si una tensión de alterna, desarrolla una cierta potencia P en una carga resistiva dada, una tensión de continua de Vrms desarrollará la misma potencia P en la misma carga, por lo tanto Vrms x I = VCA x I (véase Potencia en corriente alterna)
Fuente: http://es.wikipedia.org/wiki/Corriente_alterna#Valores_significativos
Factor de potencia
Se define factor de potencia, f.d.p., de un circuito de corriente alterna, como la relación entre la potencia activa, P, y la potencia aparente, S.1 Da una medida de la capacidad de una carga de absorber potencia activa. Por esta razón, f.d.p = 1 en cargas puramente resistivas; y en elementos inductivos y capacitivos ideales sin resistencia f.d.p = 0.
Se define el factor de potencia como:
Donde Φ es el ángulo entre la potencia activa P y el valor absoluto de la aparente S.
Si las ondas de voltaje y corriente son puramente senoidales entonces  . Φv es el ángulo del voltaje. Φi es el ángulo de la corriente.
. Φv es el ángulo del voltaje. Φi es el ángulo de la corriente.
 . Φv es el ángulo del voltaje. Φi es el ángulo de la corriente.
. Φv es el ángulo del voltaje. Φi es el ángulo de la corriente.El Factor de Potencia (FP) es la relación entre las Potencias Activa (P) y Aparente (S). Si la onda de corriente alterna es perfectamente senoidal, FP y Cosφ coinciden.
Si la onda no fuese perfecta S no estaría únicamente compuesta por P y Q, sino que aparecería una tercera componente suma de todas las potencias que genera la distorsión. A esta componente de distorsión le llamaremos D.
Supongamos que en la instalación hay una Tasa de Distorsión Armónica (THD) alta y debido a que hay corrientes armónicas. Estas corrientes armónicas, junto con la tensión a la que está sometido el conductor por el fluyen da como resultado una potencia, que si fuese ésta la única distorsión en la instalación, su valor se correspondería con el total de las distorsiones D.
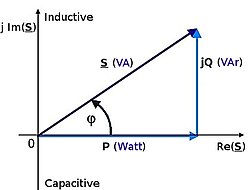
El Cosφ (Coseno de φ) no es más que el coseno del ángulo φ que forman la potencia activa (P) y la aparente (S) en el triángulo de potencias tradicional.
Si las corrientes y tensiones son perfectamente senoidales se tiene la figura 1 y por lo tanto:
Resultando que el f.d.p es el coseno del ángulo que forman los fasores de la corriente y la tensión. En este caso se puede observar que cos(<v-<I) = cos(<Z) donde Z es la impedancia equivalente del sistema. A partir de esto se puede entender el  como una medida de la habilidad del elemento Z para absorber potencia activa. Para una resistencia:
como una medida de la habilidad del elemento Z para absorber potencia activa. Para una resistencia: . Para una inductancia y condensador:
. Para una inductancia y condensador:
 como una medida de la habilidad del elemento Z para absorber potencia activa. Para una resistencia:
como una medida de la habilidad del elemento Z para absorber potencia activa. Para una resistencia: . Para una inductancia y condensador:
. Para una inductancia y condensador:
Se dice que:
- Un factor de potencia adelantado significa que la corriente se adelanta con respecto a la tensión, lo que implica carga capacitiva. Potencia reactiva negativa. 2
- Un factor de potencia atrasado significa que la corriente se retrasa con respecto a la tensión, lo que implica carga inductiva. Potencia reactiva positiva. 3
El dispositivo utilizado para medir el f.d.p. se denomina cosímetro.
FUENTE: http://es.wikipedia.org/wiki/Factor_de_potencia
Potencia aparente
La potencia compleja de un circuito eléctrico de corriente alterna (cuya magnitud se conoce como potencia aparente y se identifica con la letra S), es la suma (vectorial) de la potencia que disipa dicho circuito y se transforma en calor o trabajo (conocida como potencia promedio, activa o real, que se designa con la letra P y se mide en vatios (W)) y la potencia utilizada para la formación de los campos eléctrico y magnético de sus componentes, que fluctuará entre estos componentes y la fuente de energía (conocida como potencia reactiva, que se identifica con la letra Q y se mide en voltiamperios reactivos (var)). Esto significa que la potencia aparente representa la potencia total desarrollada en un circuito con impedancia Z. La relación entre todas las potencias aludidas es  .
.
 .
.
Esta potencia aparente (S) no es realmente la "útil", salvo cuando el factor de potencia es la unidad (cos φ=1), y señala que la red de alimentación de un circuito no sólo ha de satisfacer la energía consumida por los elementos resistivos, sino que también ha de contarse con la que van a "almacenar" las bobinas y condensadores. Se mide en voltiamperios (VA), aunque para aludir a grandes cantidades de potencia aparente lo más frecuente es utilizar como unidad de medida el kilovoltiamperio (kVA).
La fórmula de la potencia aparente es: 

FUENTE: http://es.wikipedia.org/wiki/Potencia_el%C3%A9ctrica#Potencia_aparente
POTENCIA REAL
Cuando se hizo el análisis de la potencia que consumía una resistencia (La ley de Joule), cuando era atravesada por una corriente continua, sólo era necesario multiplicar la corriente por el voltaje entre los terminales. (P = V x I)
Lo anterior también es cierto en el caso en que se utilice corriente alterna en una resistencia o resistor, porque en estos casos la corriente y el voltaje están en "fase". Esto significa que la corriente y el voltaje tienen sus valores máximos y mínimos simultáneamente (las formas de onda son iguales. Sólo podrían diferenciarse en su amplitud).
¿Pero que sucedería en un circuito que tenga "reactancia"? En este caso la corriente se adelantaría o atrasaría con respecto al voltaje y sus valores máximos y mínimos ya no coincidirían. La potencia que se obtiene de la multiplicación del voltaje con la corriente (P= I x V) es lo que se llama una potencia aparente. La verdadera potencia consumida dependerá en este caso de la diferencia de ángulo entre el voltaje y la corriente. Este ángulo se representa como Θ.
Un circuito que tenga reactancia significa que tiene un capacitor (condensador), una bobina (inductor) o ambos.
Si el circuito tiene un capacitor:
- Cuando la tensión de la fuente va de 0 voltios a un valor máximo, la fuente entrega energía al capacitor, y la tensión entre los terminales de éste, aumenta hasta un máximo. La energía se almacena en el capacitor en forma de campo eléctrico.
- Cuando la tensión de la fuente va de su valor máximo a 0 voltios, es el capacitor el que entrega energía de regreso a la fuente.
Si el circuito tiene un inductor:
- Cuando la corriente va de 0 amperios a un valor máximo, la fuente entrega energía al inductor. Esta energía se almacena en forma de campo magnético.
- Cuando la corriente va de su valor máximo a 0 amperios, es el inductor el que entrega energía de regreso a la fuente.
Se puede ver que, la fuente en estos casos tiene un consumo de energía igual a "0", pues la energía que entrega la fuente después regresa a ella. La potencia que regresa a la fuente es la llamada "potencia reactiva"
Entonces en un circuito totalmente resistivo no hay regreso de energía a la fuente, en cambio en un circuito totalmente reactivo toda la energía regresa a ella.
Ahora es de suponer que en un circuito que tenga los dos tipos de elementos (reactivo y resistivo), parte de la potencia se consumirá (en la resistencia) y parte se regresará a la fuente (por las bobinas y condensadores).
La potencia que se obtiene de la multiplicación de la corriente y el voltaje en cualquier momento es la potencia instantánea en ese momento.
- Cuando el voltaje y la corriente son positivos: La fuente está entregando energía al circuito.
- Cuando el voltaje y la corriente son opuestos (uno es positivo y el otro es negativo), la potencia es negativa y en este caso el circuito le está entregando energía a la fuente.
Se puede ver que la potencia real consumida por el circuito, será la potencia total que se obtiene con la fórmula P = I x V, (potencia entregada por la fuente, llamada potencia aparente) menos la potencia que el circuito le devuelve (potencia reactiva).
La potencia real se puede calcular con la siguiente fórmula: P = I2R
donde:
- P es el valor de la potencia real en watts (vatios)
- I es la corriente que atraviesa la resistencia en amperios
- R es el valor de la resistencia en ohmios
¿Cómo se obtiene la corriente en un circuito que tiene resistencia y reactancia?
Se utiliza el concepto de impedancia. En este caso la Impedancia de este circuito es: Z = R + jX
donde:
- R = resistencia
- X = la reactancia = XC - XL ( reactancia capacitiva - reactancia inductiva)
Entonces:
- Z = (R2 + X2)1/2 (ver Impedancia)
- I = E / Z (Tensión entregada por la fuente entre la reactancia total)
Donde:
- I = corriente en amperios
- E = tensión de la fuente
- Z = Impedancia calculada anteriormente
Lo anterior también es cierto en el caso en que se utilice corriente alterna en una resistencia o resistor, porque en estos casos la corriente y el voltaje están en "fase". Esto significa que la corriente y el voltaje tienen sus valores máximos y mínimos simultáneamente (las formas de onda son iguales. Sólo podrían diferenciarse en su amplitud).
¿Pero que sucedería en un circuito que tenga "reactancia"? En este caso la corriente se adelantaría o atrasaría con respecto al voltaje y sus valores máximos y mínimos ya no coincidirían. La potencia que se obtiene de la multiplicación del voltaje con la corriente (P= I x V) es lo que se llama una potencia aparente. La verdadera potencia consumida dependerá en este caso de la diferencia de ángulo entre el voltaje y la corriente. Este ángulo se representa como Θ.
Un circuito que tenga reactancia significa que tiene un capacitor (condensador), una bobina (inductor) o ambos.
Si el circuito tiene un capacitor:
- Cuando la tensión de la fuente va de 0 voltios a un valor máximo, la fuente entrega energía al capacitor, y la tensión entre los terminales de éste, aumenta hasta un máximo. La energía se almacena en el capacitor en forma de campo eléctrico.
- Cuando la tensión de la fuente va de su valor máximo a 0 voltios, es el capacitor el que entrega energía de regreso a la fuente.
Si el circuito tiene un inductor:
- Cuando la corriente va de 0 amperios a un valor máximo, la fuente entrega energía al inductor. Esta energía se almacena en forma de campo magnético.
- Cuando la corriente va de su valor máximo a 0 amperios, es el inductor el que entrega energía de regreso a la fuente.
Se puede ver que, la fuente en estos casos tiene un consumo de energía igual a "0", pues la energía que entrega la fuente después regresa a ella. La potencia que regresa a la fuente es la llamada "potencia reactiva"
Entonces en un circuito totalmente resistivo no hay regreso de energía a la fuente, en cambio en un circuito totalmente reactivo toda la energía regresa a ella.
Ahora es de suponer que en un circuito que tenga los dos tipos de elementos (reactivo y resistivo), parte de la potencia se consumirá (en la resistencia) y parte se regresará a la fuente (por las bobinas y condensadores).
La potencia que se obtiene de la multiplicación de la corriente y el voltaje en cualquier momento es la potencia instantánea en ese momento.
- Cuando el voltaje y la corriente son positivos: La fuente está entregando energía al circuito.
- Cuando el voltaje y la corriente son opuestos (uno es positivo y el otro es negativo), la potencia es negativa y en este caso el circuito le está entregando energía a la fuente.
Se puede ver que la potencia real consumida por el circuito, será la potencia total que se obtiene con la fórmula P = I x V, (potencia entregada por la fuente, llamada potencia aparente) menos la potencia que el circuito le devuelve (potencia reactiva).
La potencia real se puede calcular con la siguiente fórmula: P = I2R
donde:
- P es el valor de la potencia real en watts (vatios)
- I es la corriente que atraviesa la resistencia en amperios
- R es el valor de la resistencia en ohmios
¿Cómo se obtiene la corriente en un circuito que tiene resistencia y reactancia?
Se utiliza el concepto de impedancia. En este caso la Impedancia de este circuito es: Z = R + jX
donde:
- R = resistencia
- X = la reactancia = XC - XL ( reactancia capacitiva - reactancia inductiva)
Entonces:
- Z = (R2 + X2)1/2 (ver Impedancia)
- I = E / Z (Tensión entregada por la fuente entre la reactancia total)
Donde:
- I = corriente en amperios
- E = tensión de la fuente
- Z = Impedancia calculada anteriormente

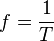







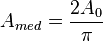
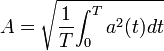
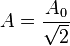




No hay comentarios:
Publicar un comentario